Raccライブラリと構文解析

• パーサ・ジェネレータとは
• 少し複雑な文法
• 四則（加減乗除）計算のBNF
• Racc で実装
  • クラス定義、BNFの記述部分
  • ヘッダー、インナー、フッター
• コンパイルと実行
• 演算子の優先順位と結合における左右の優先順位
• まとめ

パーサ・ジェネレータとは

パーサを日本語で「構文解析器」といいます。 「器」とといっても、「うつわ」ではなく「器械」、より適切にはアプリケーションまたはプログラムのことです。 つまり、構文解析をするプログラムです。

「構文解析」とは、「プログラム言語などの構文」を「解析」することです。 簡単な例として、足し算を考えてみましょう。

1+2
11+34
123+456

3つの足し算の例があります。 出てくる数字は違うものですが、どれも「数字＋数字」というパターンは変わりません。 3番めの文字列は7つの文字からなっています。

1, 2, 3, +, 4, 5, 6

この7文字はバラバラではなく、最初の3つがひとまとまりで、「123」という数字を表しており、その後「＋」という演算記号、「456」という数字が続きます。 そこで、この7文字をタイプと値のセットで、それぞれ次のようにまとめましょう。

数字, 123
+, 何でも良い
数字, 456

数字には値が必要ですが、演算記号には値がありませんから、2番めの「値」のところは何でも良いのです。 ここでは、同じ演算記号の文字列"+"にしておきましょう。 また、「数字」というタイプは、Numberの最初の3文字をとって、シンボル:NUMで表すことにします。 すると、「123+456」という7文字の文字列は

[[:NUM, 123], ["+", "+"], [:NUM, 456]]

という配列にすることができます。 これを字句解析といいます。 配列の要素の[:NUM,123]を字句またはトークンといいます。 トークンのタイプを表す:NUMなどをタイプとかトークン・カインドといいます。 配列の2番めの要素「123」は値とか、意味上の値（semantic value）などといいます。 字句解析は、構文解析には含まれないというのが一般的な考え方です。

それでは、この構文はどういうものでしょうか。 さきほど述べたように、どの式も「数字＋数字」の形です。 そこで、この式（expression）は

expression : NUM '+' NUM

と表すことができます。 式（expression）とは数字（NUM）の次にプラス（’+’）がきて、その次にまた数字（NUM）がくるというトークンの列のことである、ということです。 この記法をBNF（バッカス・ナウア・フォーム）といいます。

この構文はRaccが理解できる形にしています。

• NUMにはコロンをつけない（:NUMとはしない）
• +はシングルクォートで囲む。

足し算のトークン・カインドを新たに決めることもできますが（例えばPLUSとして、字句解析では[:PLUS, “+”]とする）、演算子はそれ自体をトークン・カインドにすることが多いです。 そのことによって、トークン・カインドの種類が多くなるのを防ぎ、プログラマーの負担を軽くする狙いがあります。 演算子をそのままトークン・カインドにするときは、

• BNFの中ではシングルクォートで囲む
• 字句解析のトークン・カインドはシンボルではなく文字列を使う（:+ではなく'+'にする）

とします。シンボルでないことには注意してください。

このように式（expression）を定義すると、最初の3つの足し算はすべてこのBNFに沿っていることがわかります。 このBNFで表されたものを、文法（grammar）といいます。

Rubyなどのプログラム言語はもっと複雑な文法を持っていますが、その文法に入力（ソースファイル）があっているかどうかは確認ができます。 あっていなければ「Syntax Error」（文法上のエラー）となります。

例えば次のような式はさきほどの足し算の文法からはSyntax Errorになります。

1+2+3
10-6
-20

• 「1+2+3」は「1+2」までは文法通りですが、そのあと「+3」があるのでシンタックス・エラー
• 「10-6」は演算子が「+」ではなく「-」なのでシンタックス・エラー
• 「-20」は数字から始まらないのでシンタックス・エラー

この3つはエラーが発見される時点が違います。 最初から順に見ていって、エラーになるところを●で表すと

1+2+●3
10-●6
-●20

黒丸の左側の要素を見た時シンタックスエラーが確定します。

少し複雑な文法

それでは、我々が普段使う足し算、引き算の計算をBNFにしてみましょう。

この計算では、数字、＋、ー、（、）の5つのトークンが必要です。 具体例を見てみましょう。

1-2+3
(1-2)+3
1-(2+3)

最初の例は後回しにして、2番めを見てみます。 これは、はじめに1と2の2つの数字を引き算し、その結果と3を加える、というもので、木構造（ツリー）で表現すると

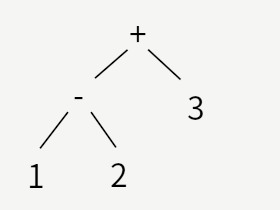
となります。 3番めは同様に、

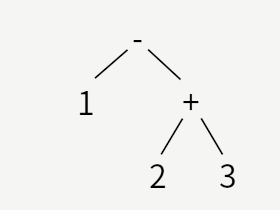
です。

1行目の「1-2+3」には括弧がないので、上の図のどちらのツリーになるか、曖昧さが残ります。 通常は頭から計算するので、1-2を先に計算するのですが、構文解析上はそれを明示する必要があります。 その方法については後ほど述べることにします。

この例では1回の計算の結果が次の式の中で使われています。 つまり、「数字＋数字」ではなく「式＋式」のような場合があるということです。 そこで、BNFを少し変えてみます。

expression : expression '+' expression | expression '-' expression

縦棒（|）は「または」という意味で、その左側のパターンでも右側のパターンでも良いということです。 このBNFでは、expressionをexpressionで定義しているので、これだけでは構文を表したことになりません。 前は式を「数字＋数字」としていました。 少なくとも数字が式の定義に出てこなければいけないでしょう。 そこで、次のように変えてみます。

expression : expression '+' expression
           | expression '-' expression
           | NUM

このように、定義は2行以上に渡っても良いことにします。 式は「式＋式」または「式ー式」または「数字」のいずれかに一致すれば良い、ということです。 これならば、「1-2+3」は式であることがわかります。

• 「1」は「数字」したがって「式」でもある
• 「1-2」は「式ー数字」だが、数字は式でもあるので、「式ー式」になる。これはBNFの2行目のパターンなので式とみなせる。
• 「1-2+3」は「1-2」が式なので、「式＋３」すなわち「式＋数字」だが、数字は式だから「式＋式」となり、BNFの1行目のパターンに一致するから式である。

しかし、実は違う方法で式であることも説明できます。

• 「1-2+3」は「2+3」が「数字＋数字」、すなわち「式＋式」だから、式となる
• 「1-2+3」は「2+3」が式なので、「数字ー式」となり、数字は式だから「式ー式」となり、BNFの2行目のパターンに一致するから式である。

１−２＋３が式であることはBNFで確認できるが、その方法は少なくとも2通りあるということです。 しかも、その計算結果は異なり、それぞれ２と−４になります。 ですから、BNFの解釈が2通りというのはとてもまずいことなのです。 また、この2通りは、さきほど木構造で表した2通りと同じことだとわかります。 ですから、解釈が1通りになるには括弧を加える、というのはひとつの方法です。

expression : expression '+' expression
           | expression '-' expression
           | '(' expression ')'
           | NUM

これだと、「（１−２）＋３」や「１−（２＋３）」が文法的に合うようになります。 解釈が2通り出てしまう「１−２＋３」は防げませんが、そういうものは

• シンタックス・エラーだということにする
• 解釈が2通りでたら「左側の演算から優先的に行う」という条件をつけて1通りに強制する

のどちらかを採用すればよいのです。

また、次のようにBNFを変更すると、常に計算は左から行われるようになります。

expression : expression '+' primary
           | expression '-' primary
           | primary
primary    : '(' expression ')'
           | NUM

「１−２＋３」がこれでどのように解釈されるか考えてみましょう。 なお、primaryは日本語で一次因子とかプライマリーと呼ばれます。

• 「１−２」は「数字ー数字」で、数字＝＞プライマリー＝＞式だから、「式ープライマリー」なので式になる
• 「１−２＋３」は「式＋３」すなわち「式＋数字」になり、それは「式＋プライマリー」だから「式」になる

２＋３を先に計算する方は上記のBNFには合いません。

• 「２＋３」は「数字＋数字」＝＞「式＋プライマリー」になるので「式」になる
• 「１−２＋３」は「数字ー式」＝＞「式ー式」になるが、「式ープライマリー」ではない。したがって、式にはならない

このBNFは計算の第二項が「式」ではなく「プライマリー」であるとして、プライマリーが「括弧で囲まれた式」か「数字」のみということで、括弧なしで右から計算することを取り除いています。

以上をまとめると、計算の順序の曖昧さを防ぐ方法は2つあり、

• BNFで示す
• 演算子＋とーが2つあった場合、左から計算すると定義しておく

ということになります。

四則（加減乗除）計算のBNF

今回の最後に四則計算の文法定義のBNFを作ってみましょう。 足し算引き算のところで、演算子が2つあったとき、左から計算するか、右から計算するかの2通りの解釈が生まれる場合がありました。 似たものに、乗除と加減の優先順位の問題があります。

1+2*3

ここでは、Rubyと同じように掛け算はアスタリスク（*）で表します。 この計算では、「２かける３」を先にやることになっています。 ですから、

1+2*3 = 1+6 = 7

となります。 これは小学校で習いますね。 ところが、コンピュータはそういうことを習っていませんから、BNFなどで、演算の優先順位を定義しなければなりません。 ところで、「１＋６」の１や６を「項（term）」と呼びます。 また、「２＊３」の2や3を「因子（factor）」といいます。 BNFだけで演算の優先順位を表現するには式、項、因子を分けて定義します。

expression  : expression '+' term
            | expression '-' term
            | term
term        : term '*' factor
            | term '/' factor
            | factor
factor      : '(' expression ')'
            | NUMBER

このBNFは「2+3+4」のような括弧のない式は左から順に計算するようになっており、曖昧さが発生しません。 このBNFでは、単項マイナス、すなわち因子の符号を変えるマイナス（例えば「−２」のようなマイナス）はサポートしていません。

Racc で実装

このBNFをRaccのソースファイルに取り入れて、コンパイルしてみましょう。 Raccのソースファイルは拡張子.yにするのが習慣です。 大きく4つのパートに分かれます。

• クラスの定義、BNFの記述部分。この部分はRaccによってRubyプログラムにコンバートされる
• （header）クラス定義の前にコピーされるRubyプログラム
• （inner）クラスの中のコンバートされる部分の前に挿入されるRubyプログラム
• （footer）クラス定義のあとにコピーされるRubyプログラム。メインプログラムを書く場合はここに書く

クラス定義、BNFの記述部分

ここがRaccのソースプログラムのメインです。 スーパークラスは書かないようにします（class A < BのBの部分は書かない）。

• token の後にトークンを宣言しておく。これは無くても良いが、トークンの綴間違いなどをチェックできる。例えば token NUMのようにする
• optionsの後にオプションを指定できる。options no_result_varが良く用いられる。その意味はドキュメントを参照
• rule以降（classのendまで）にBNFを記述する

具体例を次に示します。

class Sample1
  token NUMBER
  options no_result_var
rule
  expression  : expression '+' term { val[0] + val[2] }
              | expression '-' term { val[0] - val[2] }
              | term
  term        : term '*' factor { val[0] * val[2] }
              | term '/' factor { if val[2] != 0 then val[0] / val[2] else raise "Division by zero." end }
              | factor
  factor      : '(' expression ')' { val[1] }
              | NUMBER
end

BNFは加減乗除をサポートする以前示したものと同じですが、その後ろに波括弧で囲まれた部分があります。 これはアクションと呼ばれるものです。 アクションの左側のBNFに一致したときに、そのアクションが実行されます。 配列valは左のBNFの要素に対応するアクションが実行されたときの結果です。 例えば

  factor      : '(' expression ')' { val[1] }
              | NUMBER

この2行目にはアクションがありませんが、その場合のアクションは{ val[0] }、すなわち最初のBNFの要素のアクションの結果を返す、ということになっています。 NUMBERは字句解析で返された数字に一致しますので、その値が返されます。 1行目は括弧で囲まれた式です。このBNFには、左括弧、式、右括弧の3つの要素があります。val[1]は2番めの要素である式のアクションの結果です。 したがって、この括弧で囲まれたfactorの値は、括弧で囲まれた式の値になります。

このようにして、それぞれの式に一致したときに、その計算がアクションとして行われます。

なお、定義するクラスをモジュールの中に入れたいときは

class MName::Sample1

のようにします。MNameはクラスを入れるモジュールの名前です。 Raccでコンパイルすると

module MName
  class Sample1
... ... ...
  end
end

このようになります。

ヘッダー、インナー、フッター

ヘッダーに良く書かれるのはrequire文です。 このサンプルプログラムでは特に記述するものはありません。

インナーには字句解析関係のプログラムを書きます。 また、Raccで生成したパーサが字句を一つずつ読み込むためのメソッドはnext_tokenというメソッド名に決まっています。 それを実装します。具体例を示します。

def lex(s)
  @tokens = []
  until s.empty?
    case s[0]
    when /[+\-*\/()]/
      @tokens << [s[0], s[0]]
      s = s[1..-1] unless s.empty?
    when /[0-9]/
      m = /\A[0-9]+/.match(s)
      @tokens << [:NUMBER, m[0].to_f]
      s = m.post_match
    else
      raise "Unexpected character."
    end
  end
end

def next_token
  @tokens.shift
end

メソッドlexが引数の文字列を字句解析するプログラムです。 ここでは、StrScanライブラリを使っていませんが、大きなプログラムでは高速な字句解析のためにStrScanを用いるほうが良いです。 その場合は、headerのところにstrscanライブラリをrequireしてください。 演算子は、その文字列をタイプと値にして@tokensにプッシュします。 数字（0以上の整数）はタイプを:NUMにしてその数字（Floatオブジェクトに直したもの）をプッシュします。 IntegerでなくFloatにしたのは、割り算で小数点以下まで出したかったからです。 Integerオブジェクトにしても良いのですが、その場合は割り算で小数点以下は切り捨てられます。 それ以外の文字は例外を発生させます。

メソッドnext_tokenは字句解析の配列からひとつづつ取り出して返します。

フッターの部分にはメインプログラムを書きます。 メインプログラムから構文解析プログラムを呼ぶにはメソッドdo_parseを用います。 そのメソッドを呼ぶ前にはlexメソッドで字句解析を終えていなければなりません。 以下の例では一行入力しては、その計算をして表示します。

sample = Sample1.new
print "Type q to quit.\n"
while true
  print '> '
  $stdout.flush
  str = $stdin.gets.strip
  break if /q/i =~ str
  begin
    sample.lex(str)
    print "#{sample.do_parse}\n"
  rescue => evar
    m = evar.message
    m = m[0] == "\n" ? m[1..-1] : m
    print "#{m}\n"
  end
end

特に難しいことないと思います。 ソースプログラム（sample1.y）の全体も以下に示しておきます。

class Sample1
  token NUMBER
  options no_result_var
rule
  expression  : expression '+' term { val[0] + val[2] }
              | expression '-' term { val[0] - val[2] }
              | term
  term        : term '*' factor { val[0] * val[2] }
              | term '/' factor { if val[2] != 0 then val[0] / val[2] else raise "Division by zero." end }
              | factor
  factor      : '(' expression ')' { val[1] }
              | NUMBER
end

---- header

---- inner

def lex(s)
  @tokens = []
  until s.empty?
    case s[0]
    when /[+\-*\/()]/
      @tokens << [s[0], s[0]]
      s = s[1..-1] unless s.empty?
    when /[0-9]/
      m = /\A[0-9]+/.match(s)
      @tokens << [:NUMBER, m[0].to_f]
      s = m.post_match
    else
      raise "Unexpected character."
    end
  end
end

def next_token
  @tokens.shift
end

---- footer

sample = Sample1.new
print "Type q to quit.\n"
while true
  print '> '
  $stdout.flush
  str = $stdin.gets.strip
  break if /q/i =~ str
  begin
    sample.lex(str)
    print "#{sample.do_parse}\n"
  rescue => evar
    m = evar.message
    m = m[0] == "\n" ? m[1..-1] : m
    print "#{m}\n"
  end
end

コンパイルと実行

コンパイルは「racc ソースファイル名」で行います。

$ racc sample1.y
$ ls
sample1.y sample1.tab.rb

sample1.tab.rbがRaccで生成されたRubyプログラムです。 このファイルをエディタで見ると、BNFが様々な配列とメソッドに変換されているのがわかります。 実行してみましょう。

$ ruby sample1.tab.rb
Type q to quit.
> 1-2-5
-6.0
> 2*3+4*5
26.0
> (10+25)/(3+4)
5.0
> q

計算は正しく行われていますね。

演算子の優先順位と結合における左右の優先順位

BNFにあいまいさがあるときに、その解決方法として

• BNFをあいまいさの残らない形に変更する
• 演算の優先順位を指定する

の2つが考えられます。 後者には2つあり、例えば

• 乗除は加減より優先的に計算する。例えば「１＋２＊３」では「１＋２」よりも「２＊３」を先に計算する。 このように演算子の間に優先順位をつけることにより、曖昧さを解決できることがあります。 四則では、
  • 乗除の優先順位は同じ。つまり「１＊２／３」は「１＊２」と「２／３」のどちらを先にするかの取り決めはない。この順については別に定めが必要
  • 加減の優先順位は同じ。
  • 乗除は加減に対して優先順位が高い
• 同レベルの演算があったときに、左から先に計算する（左結合）または右からさきに計算する（右結合）を定める。 通常は加減乗除とも同レベルの演算は左から先に計算する。 右結合は少ないが、無いわけではない。たとえば累乗は右結合である。累乗を「＾」で表すと「２＾３＾４」は「２＾８１」のことになる。

Raccでは、これらの優先順位を指定することができます。 優先順位をprecedenceといい、Raccはこの最初の4文字を用いて

• prechigh: 優先順位が高い
• preclow: 優先順位が低い

この2つ間に演算子を書き、同じ行には同じ優先順位、上の方が優先順位が高い、とします。

また、左結合はleft、右結合はrightで指定します。 以上のルールを用いると、BNFが単純でもパーサを生成することができます。

Raccのソースファイルの最初の部分を書き換えてみましょう。 なお、footerのインスタンス生成時のクラス名はSample1からSample2に変更が必要です。

class Sample2
  token NUMBER
  prechigh
    left '*' '/'
    left '+' '-'
  preclow
  options no_result_var
rule
  expression  : expression '+' expression { val[0] + val[2] }
              | expression '-' expression { val[0] - val[2] }
              | expression '*' expression { val[0] * val[2] }
              | expression '/' expression { if val[2] != 0 then val[0] / val[2] else raise "Division by zero." end }
              | '(' expression ')' { val[1] }
              | NUMBER
end

3行目から6行目が計算順を示す部分です。 このおかげで、BNFは短く、すっきりしたものになりました。

まとめ

この電卓プログラムのソースコードはわずか57行です。 これをRubyで書いたら、そんな短いコードではすみません。

Raccは構文解析が必要なプログラム、例えばインタープリタ、コンパイラ、電卓などを書くときの大きな手助けになります。 言語はCで書かれることが多いですが、Cの場合はパーサ・ジェネレータのBisonを使うことが多いです。 BisonもRaccのようなプログラムです。

Raccを使った電卓プログラムをGitHubにあげてありますので、参考に見てください。

https://github.com/ToshioCP/calc

また、Raccのドキュメントはこちらをご覧ください。

https://i.loveruby.net/ja/projects/racc/doc

• 2023 8
• 2022 37